Notes from a new user
Back to main tutorial pages
(Courtesy of Katie Abley, JIC)
Overview
GFtbox is a tool for modelling the genetic control of tissue growth which allows the incorporation of gene regulatory networks and signal propogation within a growing, mechanically connected, tissue.
In GFtbox, tissue is treated as a continuous sheet of material with two surfaces and a thickness, here termed the canvas. Within the canvas regionally expressed factors under genetic control may interact and propagate.
Polarity is established by signals that propagate through the tissue and is anchored in genetically controlled regions termed tissue polarity organisers. Rates of growth parallel or perpendicular to the local polarity may be specified through a regulatory network.
The resulting growth of the canvas depends on how specified growth patterns interact within the constraints of mechanically connected tissue. Within GFtbox, elasticity theory is used to compute this resultant deformation of the canvas. Mechanical constraints lead to emergence of features such as curvature that were not directly specified by the regulatory networks. Resultant growth feeds back to influence spatial arrangements and local orientations of tissue, allowing complex shapes to emerge from simple rules.
Projects
Structure
Each project has a name that begins with GPT_. The projectname has three parts: 'GPT_*_yyyymmdd' where * refers to the name you choose, the prefix and suffix are added automatically. 'GPT' stands for Growing Polarised Tissue, suffix is the date). A new project contains the main data structure 'ProjectName.mat', a work file 'ProjectName_static.mat' and a subdirectory, 'snapshots', with an image of the initial mesh. The initial files are augmented by the interaction function 'projectname.m', some working files and results. The results include stage files, snapshots and movies.
Structure of the interaction function
The information about models in GFtbox is held in two places. The first is a data structure called 'm'. For example, this structure contains matrices which hold information about the x, y and z co-ordinates of each node (the matrix 'm.nodes') and about factor concentrations at each node (the matrix 'm.morphogens'). The second is the interaction function - a Matlab function. The interaction function is automatically kept in synch with the internal data structure by GFtbox.
Within one interaction function, multiple variants of the same model can be created. These variants might, for example, be models of the wild type (WT) scenario and of one or mutants. The variants of the model need to be named. This can be done with the following bit of code:
Where'SQUARE', 'CIRCLE', 'OFFCIRCLE' are the names of the variant models and the value given to 'm.userdata.ranges.modelname.index =' in the line below specifies which entry in the string {'SQUARE', 'CIRCLE', 'OFFCIRCLE'} should be run. Here, to run SQUARE, 1 should be used; for CIRCLE, 2; and for OFFCIRCLE, 3.
Overview of different parts of the code and how it is organised. (What is the significance of @@ - these are not yet fully operational - they are commands that enable us to automatically generate a mathematical represention of the Matlab using Latex).
Each project may have several models - explain how they are done.
Time dependent steps. Create a time-modulated identity factor.
Saving
If you wish to create a model from scratch, once you have created a mesh in the growth toolbox, you can save the project by clicking Save As. Make a new folder for your project wherever you want to save it. The name of the folder will start with GPT (growing polarised tissue), will be followed by the date (year, month, day). For example: GPT_101115_ArabidopsisLeaf.
Once you have saved the project folder, an matlab m.file will automatically be produced when you click Edit (in the GUI). By clicking Notes you can also produce a text file of the same name into which you can write notes. The name of the folder must be appropriate for matlab - this will be the case if you use underscores in the name.
Loading
Use the load button in the GUI to load a previously saved project. Or, Menu:Projects allows you to specify a folder for models and select a project from this folder.
Growth Programs
When building a model, a mesh of finite elements (the canvas which represents the tissue being modelled) needs to first be created. Then, the initial state of the canvas needs to be specified. This may involve assigning particular identities (identity factors) to local regions of the canvas and specifying initial signals (signalling factors) which can propogate through the canvas.
In order to specify growth, a polariser regulatory network (PRN) must be created. The PRN controls the activity of various organisers from which tissue polarity information propagates. Polarity propagation is implemented through a signalling factor called POLARISER (POL), the gradient of which defines local polarity. The PRN controls production and degradation of POL at organisers that anchor the polarity.
A growth rate (K) regulatory network (KRN)must also be created which defines how identity or signalling factors influence specified growth rates (i.e. strain rates) in relation to local polarity. For each region there are two specified growth rates in the plane of the canvas – a rate parallel to the local polarity, termed Kpar, and a rate perpendicular to the local polarity, termed Kper. These specified growth rates can be enhanced or reduced on either surface of the canvas (termed the A and B surfaces). A third specified growth rate Knor is used to define the rate of growth in tissue thickness.
For models incorporating gene interactions, a gene regulatory network (GRN) is defined that controls the activity of identity or signalling factors encoded by known genes. The genes within the GRN influence growth by modulating the PRN and the KRN.
During simulations, the interaction of the specified growth (determined by the regulatory networks described above) with the mechanical constraints of the canvas are calculated, allowing resultant growth to be predicted.
Below, explanations of how to direct GFtbox to perform the above functions are given.
Setup
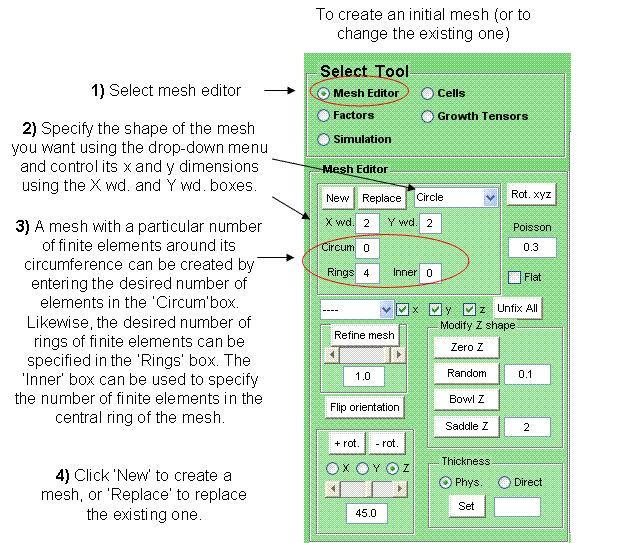
Establishing a Mesh
Once you have created an initial mesh, a number of its properties can be modified.
The number of finite elements in the mesh can be increased using the refine mesh button. This subdivides a given proportion of all the edges in the mesh and the proportion of edges to be subdivided can be specified below the refine mesh button.
The shape of the canvas along the z axis can be controlled using the panel 'Modify z shape'. Pressing the button 'Zero Z'makes the canvas completely flat along the z axis but enables it to deform along this axis during simulations (it doesn't constrain the canvas to stay flat).
The 'Random' button causes the z co-ordinate of each node in the mesh to vary during the simulation, by an amount specified in the box adjacent to 'Random'. Adding this randomness to the values of the z co-ordinates makes it easy for the canvas to deform along the z-plane during growth. The buttons 'Saddle Z' and 'Bowl Z' curve the mesh (in opposite directions) and the direction of this initial bend will most-likely be maintained during growth.
If the check-box 'Flat' is ticked this will force the mesh to remain flat (not to bend in the z direction) throughout the simulation.
The panel with the buttons '+ rot' and - 'rot' allows the orientation of the canvas to be controlled.
The thickness of the canvas (along the z axis) can be controlled using the 'Thickness' panel. 'Physical' thickness represents the specified thickness of the canvas and should be used by default. 'Direct' thickness represents the resultant thickness, and shouldn't be used.
The box 'Poisson' contains the poisson ratio for the canvas. When a block of material is compressed by external forces in one direction, Poisson’s ratio is the ratio of its transverse expansion to its longitudinal compression. The default value should not be changed as it is thought to be ideal for leaf tissue.
Creating Factors
Within the GFtbox a number of factors involved in specifying growth are automatically present. The names of these factors can be viewed in the drop-down menu entitled 'Plot current factor'. Selecting a factor from this list causes its distribution across the canvas to be displayed.
KAPAR (or KBPAR) is a growth factor which specifies the growth rate of nodes on face A (or B) of the canvas in the direction that is parallel to the polariser gradient.
KAPER (or KBPER) is a growth factor which specifies the growth rate of nodes on face A (or B) of the canvas in the direction that is perpendicular to the polariser gradient
KNOR is a growth factor which specifies the rate of growth of the canvas thickness
POLARISER is a factor which provides directional information (polarity) to local regions of the canvas via its concentration gradient
STRAINRET is a factor which determines to what extent the strain arising from growth is retained. Note that, by default, the strain arising from growth is discarded at each time step of the simulation.
ARREST is a factor which causes arrest of cell division. This is only relevant if you have imposed a layer of cells upon the canvas.
New factors can be added to this list in the following way:
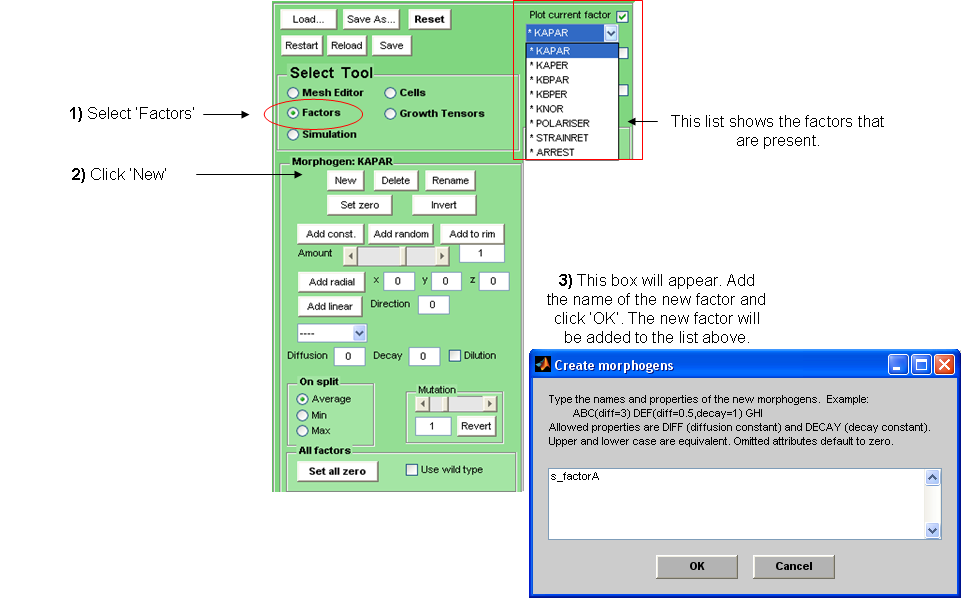
Factors should be named using the following prefices according to their role during growth:
id_ for identity factors (non-diffusible factors that specify local tissue identities
s_ for signalling factors (factors that can diffuse through the canvas but are not polarisers)
in_ for non-diffusible initialisation factors (factors which are used for intial growth of the canvas to get the canvas to the starting state from which modelling will really begin).
is_ for diffusible initialisation factors
Within the 'm' structure, there is a matrix called m.morphogens which has a column for each factor and a row for each node position in the matrix. A value for each morphogen at each node is held in this matrix. When a new factor is added in the way described above, a column for this factor is added to the m.morphogens matrix.
Initialisation
By clicking
In factors tab in the GUI can be used to assign properties to each factor that is specified in the model. It is important to note that if you want to assign properties to factors using the GUI, the following part of the interaction function must be commented out, otherwise the changes you make using the GUI won't work.
% In this section you may modify the mesh in any way whatsoever.
%if Steps(m)==0 %
%m.morphogens(:) = 0;
%m.morphogenclamp(:) = 0;
%m.mgen_production(:) = 0;
%m.mgen_absorption(:) = 0;
%m.seams(:) = false;
%m.mgen_dilution(:) = false;
The amount of a given morphogen added to the canvas can be specified using the 'amount' bar. The factor can be added at a constant concentration throughout the canvas by clicking the 'add constant' tab.
Lesson 1: Using the interaction function to specify identity regions, signal production and decay, and istropic growth in particular regions.
Opening the interaction function and where to start.
In the interaction function, the ways different factors interact can be specified. The interaction function can be used to assign specific identities to local regions of the canvas and to specify initialisation signals. This is important for setting up the polariser and growth factors which will themselves direct growth.
To initialise the model using the interaction function, in the panel entitled 'Interaction function', click on the 'Edit' button. This will open the matlab editor.
Within the interaction function there are lots of instructions (in green) about which parts of the code can be modified. Examples of what one might like to do in each section of the interaction function are also provided.
Here the specification of initial local identity domains that have either a central square shape, a central circle shape, or an off-centre circle shape, is demonstrated. How to position the source of a signal in a particular identity region is also shown, as are ways to position sinks that degrade the signal, producing different types of signal gradients. How to specify isotropic growth in particular regions of the tissue is also shown.
To demonstrate these different things, variant models have been specified in the same interaction function. To set up the different model variants, use the following code format in the part of the interaction function where the comments direct you set up model variants:
% Set up names for variant models. Useful for running multiple models on a cluster.
m.userdata.ranges.modelname.range = ...
{ 'SQ_IN_CIRCLE', ...
'CENTRE_OF_CIRCLE', ...
'OFFCENTRE_CIRCLE', ...
'CENTRE_SOURCE', ...
'CENTRE_SOURCE_2', ...
'SOURCE_SINK', ...
'SOURCE_SINK_2', ...
'SOURCE_SINK_2_GROWTH', ...
'SOURCE_SINK_2_GROWTH_BOWL' };
m.userdata.ranges.modelname.index = 9;
% CLUSTER. This is where you choose which variant to run.
% Using the number 9 causes the 9th model in the
%list, 'SOURCE_SINK_2_GROWTH_BOWL', to be run
end
In the main part of the model where you are specifying the differences between the variants, you should use a switch statement, for example like this:
switch modelname
case 'SQ_IN_CIRCLE'
%code specific to this model variant
case 'CENTRE_OF_CIRCLE'
%code specific to this model variant
case 'OFFCENTRE_CIRCLE'
%code specific to this model variant
case 'CENTRE_SOURCE'
end
Using model variants within an interaction function is useful if you wish to model a wild-type developmental situation involving several different factors, and one or more mutant situations where only one of the factors has been altered from the wild-type model. Using variants of a model to represent mutants allows you to just make small modifications to the WT model for mutants whilst still using exactly the same code for most of the model.
Initialisation steps should be specified in the part of the interaction function where the following code is:
The m.nodes matrix
The positions of all vertices of the mesh are held in a matrix called m.nodes. m is a structure which holds all of the information about the canvas and nodes is one matrix within the structure m. Nodes is an nx3 matrix where each row represents a different vertex and the three columns represent the x,y,z coordinates of that vertex.
The matrix m.nodes may be viewed by putting a break point at a line of code where m.nodes appears in the interaction function and running the simulation until the break point. Then, by highlighting 'm.nodes' and pressing F9 (or right clicking on the highlighted 'm.nodes' and choosing evaluate), the m.nodes matrix will be displayed in the matlab command window.
To assign a particular identity factor to local regions of the matrix, values of either 1 or 0 for that identity factor need to be assigned to each node of the matrix. The X coordinates of every vertex are given by m.nodes(:,1), the Y coordinates are given by m.nodes(:,2) and the Z coordinates by m.nodes(:,3).
Example 1: Specifying a central square identity region
To assign an identity factor (called id_centre, added by creating a new factor with the GUI), to a square centred on the centre of the canvas, the following code can be used in the appropriate model variant case in the initialisation:
case 'SQ_IN_CIRCLE'
SQUARE_RADIUS =0.5
is_centre_region = (abs(m.nodes(:,1))< SQUARE_RADIUS)...
& (abs(m.nodes(:,2))< SQUARE_RADIUS);
id_centre_p(is_centre_region) = 1
id_centre_l = id_centre_p * id_centre_a;
First the distance from the centre of the square to its edge is defined (using SQUARE_RADIUS = 0.7;). Then, the variable 'is_centre_region' is given a value of 0 or 1 for all of the nodes in the canvas with the code 'is_centre_region = (abs( m.nodes(:,1) ) < SQUARE_RADIUS)& (abs( m.nodes(:,2) ) < SQUARE_RADIUS);
This means 'is_centre_region' will be 1 only for nodes where the absolute value (abs) of the X coordinates of the vertex (m.nodes(:,1)) are less than the value of'SQUARE_RADIUS' and the absolute value (abs) of the Y coordinates of the vertex( m.nodes(:,2))are also less than 'SQUARE_RADIUS'.
This creates a boolean vector (containing only 0s and 1s) entitled 'is_centre_region'. The values in this vector (there is one for each node of the canvas)can be viewed in the command window by putting a break point at the line of code including 'is_centre_region',stepping the simulation, highlighting 'is_centre_region' and then pressing F9.
The initialisation identity factor, id_centre, is assigned to the same nodes that is_centre_region was assigned to using the code:
id_centre_p(is_centre_region) = 1;
This bit of code says that the 'id_centre' vector (the id_centre column in the m.morphogen matrix) should be given the same boolean vector that is_centre_region has been assigned.
Note that id_centre is folowed by _p. In the interaction function, each factor can appear with one of four different suffices:
_p = level of factor. This gets updated at the end of the interaction function and might change according to growth. This suffix should be used when the factor appears on the left hand side of an equation. The p means promoter level - how much the expression of the factor is being promoted in the model.
_i = index. Each morphogen has it's own index for storing growth information in global morphogen structures.
_l = effective level. This suffix should be used when the factor appears on the right hand side of an equation. In constrast to p, which represents promotion of a factor, l should be used to represent the total amount of functional product as a result of gene expression.
_a = expression level. If a factor has the suffix 'a', its expression level can be controlled using the Mutation box in the factors tab of the GUI. Changing the value of expression from 1 in the mutation box can be used to model mutants with increases or decreases in the expression of a given factor. Clicking the 'Revert' button will make the level of the factor return to 1.
The line:
id_centre_l = id_centre_p * id_centre_a;
sets the effective level of id_centre to be equal to the promotion of id_centre (id_centre_p) multiplied by the expression level of id_centre (id_centre_a).
Example 2: Specifying a central circular identity region
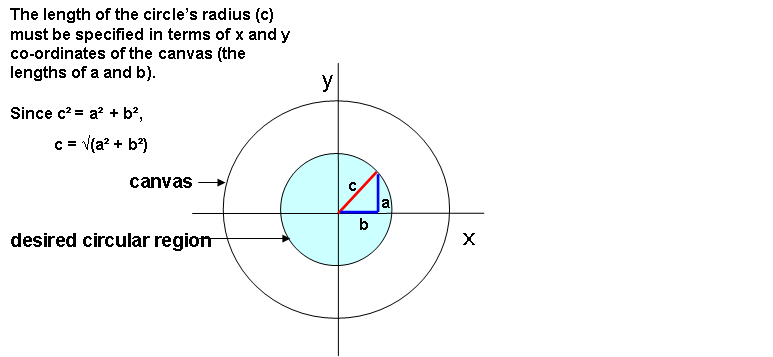
To specify a circle with a radius of 0.5 (for example) centred on a particular point, rather than just selecting nodes that are between - 0.5 and + 0.5 along the x axis and the y axis, which produces a square, we need to select nodes that are less than a radius of 0.5.
To incorporate this into the interaction function, the following bit of code can be used:
case 'CENTRE_OF_CIRCLE' % name of the model variant
CENTRE_RADIUS = 0.5; % radius of the central region
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
% calculating radii using pythagoras's theorem
id_centre_p(radii <= CENTRE_RADIUS) = 1;% setting the promotion of the factor id_centre to be
% 1 wherever the radii is less than CENTRE_RADIUS
id_centre_l = id_centre_p * id_centre_a;% sets the effective level of id_centre_l to
% be equal to the promotion of
% id_centre * the expression
% level (given by the value of id_centre_a.
Example 3: Specifying an off-centre circular identity region.
To displace a circle away from the centre of the canvas, the following code can be used:
case 'OFFCENTRE_CIRCLE'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ]; % the x, y co-ordinates of the position of the
% centre (due to its displacement from 0,0).
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
% the x and y co-ordinates of the new centre
%point are
% subtracted from the x and y co-ordinates of the
% m.nodes positions used in the radii
% calculation
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
Example 4: Producing a diffusable signal from the central identity region and specifying an equal rate of decay everywhere in the canvas.
To achieve this task, first a signal factor needs to be added to the model using the GUI. In the factors part of the GUI, the signal's diffusion rate can be set in the diffusion box. Here a value of 0.5 was used for the signal created (s_centre).
The following bit of code in the initialisation part of interaction function can be used to set the soure to be produced in the same place as the circular id_centre specified in example 2.
case 'CENTRE_SOURCE'
CENTRE_RADIUS = 0.5; %this is the same code as for example2
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
m= leaf_mgen_conductivity(m,s_centre_i, 0.5);
% this sets the diffusion rate of s_centre_i
m.mgen_production( :, s_centre_i ) = 0.1*id_centre_l;
% In all the rows of the s_centre_i column of the m.mgen production array,
% the value of s_centre_i is set to 0.1*the effective level of id_centre_l.
% this means that s_centre is produced by id_centre at a rate of 0.1.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
% This causes s_centre to decay everywhere at a constant rate
% proportional to its concentration and proportional to the time step, so that
% if the time step is 0.01, then 10*0.01 is 0.1 and s_centre will decay by 0.1
% ie. 10% of its concentration each time step.
Example 5: Fixing the amount of a diffusable signal in a given area.
In biological systems, homeostatic mechanisms ofter exist to keep the concentration of a particular factor constant in a particular area. To simulate this in the growth toolbox, we can use a function called morphogenclamp to fix the level of a factor in a certain area. When this function is used, the factor remains free to diffuse into the area where its concentration is not fixed. The following code can be used to fix the concentration of s_centre to 1 everywhere that id_centre is 1 (ie in the circular central identity region).
case 'CENTRE_SOURCE_2'
CENTRE_RADIUS = 0.5;
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
s_centre_p( id_centre_l > 0 ) = 1;
m.morphogenclamp( id_centre_l > 0, s_centre_i) = 1;
%s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
% The morphogenclamp function should be assigned a boolean value
%(1 if you want to clamp the morphogen, 0 if you don't).
% The first argument given to the function (id_centre_l>0)
% gives the nodes of the mesh where the function should apply,
% the second argument gives the morphogen to be
% clamped.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
Example 6: Positioning a sink for the diffusable signal at the rim of the canvas.
To achieve this task, a rim identity region (called id_rim here) should be set up using the GUI. Here, the morphogenclamp function has been used to set the value of s_centre to 0 wherever id_rim is present. This causes the rim to act as a sink since any signal that diffuses into it will effectively disappear. This model quickly creates a stable linear gradient of s_centre between the id_centre and the id_rim region providing that the diffusion rate is quick enough.
case 'SOURCE_SINK'
CENTRE_RADIUS = 0.5; %previously used code
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
% rimnodes is assigned the positions
%where radii is bigger than the maximum radii * 0.8
id_rim_p( rimnodes ) = 1;
% id_rim is set to 1 in the same place as rimnodes
id_rim_l = id_rim_p * id_rim_a;
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
Example 7: Combining production of a source in an off-centre circle with a rim around the sink .
The following code is a combination of the different examples given above. It specifies an off-centre circular identity region, causes a diffusible signal to be maintained at a constant level wherever the circular identity region is present, specifies a rim identity region and sets the concentration of the diffusible signal to 0 at the rim.
case 'SOURCE_SINK_2'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
Example 8: Adding isotropic growth.
To add isotopic growth wherever the id_centre region exists in the last model variant outlined above, a new case can be made with exactly the same intialisation code as for the the last model variant described:
case 'SOURCE_SINK_2_GROWTH'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
Additionally, the following bit of code to specify growth rates should be added to the part of the model labelled %Code for specific models.
% Code for specific models.
switch modelname
case { 'SOURCE_SINK_2_GROWTH', 'SOURCE_SINK_2_GROWTH_BOWL' }
kapar_p = 0.1 * pro( 1, id_centre_l );
kbpar_p = kapar_p;
kaper_p = kapar_p;
kbper_p = kaper_p;
Here, kapar (the rate of growth parrallel to a polariser that doesn't exist here) is set to be 0.1 everywhere, but promoted by the effective level of id_centre by a scalar factor of 1 using *pro(1, id_centre_l). This promotion by id_centre_l means that kapar will be 0.1 everywhere in the canvas where id_centre is absent, and will be 0.2 in the presence of id_centre. kbpar (the rate of growth parrallel to a non-existent polariser on the other side of the canvas to where kapar applies) is set to the value of kapar. The perpendicular growth rates on each side of the canvas(kaper_p and kbper_p) are also set to be the same as kapar. This produces isotropic growth of the canvas, at double the background rate where id_centre is present.
If this model is run with the canvas initially having random z displacements (as described in the mesh section) random deformations above and below the initial canvas surface will be produced.
Example 9: Growth with the canvas initialised in a bowl shape to bias the 3D deformation.
To bias the 3D deformation of the canvas in a particular direction, the following code can be used in the appropriate intialisation case:
case 'SOURCE_SINK_2_GROWTH_BOWL'
m = leaf_setzeroz( m );
m = leaf_bowlz( m, -0.1 );
All code for lesson 1
Below is all the code (the whole interaction function) used to create the model variants that have been described in this lesson. Please note that the first example interaction function given below is not organised in the ideal way, although it is the easiest way to see how each model variant works. Please look at the second example interaction function below to see the best way to organise this code.
Example code 1
function m = gpt_circle_101118( m )
%m = gpt_circle_101118( m )
% Morphogen interaction function.
% Written at 2010-11-19 10:06:32.
% GFtbox revision 3254, 2010-11-18 20:25:53.442272.
% The user may edit any part of this function between delimiters
% of the form "USER CODE..." and "END OF USER CODE...". The
% delimiters themselves must not be moved, edited, deleted, or added.
if isempty(m), return; end
fprintf( 1, '%s found in %s\n', mfilename(), which(mfilename()) );
if exist( 'local_setproperties' )
m = local_setproperties( m );
end
realtime = m.globalDynamicProps.currenttime;
%%% USER CODE: INITIALISATION
% In this section you may modify the mesh in any way whatsoever.
if Steps(m)==0 % First iteration
% Zero out a lot of stuff to create a blank slate. If you want to use the
% GUI to set any of these things in the initial mesh, then you will need to
% comment out the corresponding lines here.
m.morphogens(:) = 0;
m.morphogenclamp(:) = 0;
m.mgen_production(:) = 0;
m.mgen_absorption(:) = 0;
m.seams(:) = false;
m.mgen_dilution(:) = false;
% Set up names for variant models. Useful for running multiple models on a cluster.
m.userdata.ranges.modelname.range = ...
{ 'SQ_IN_CIRCLE', ...
'CENTRE_OF_CIRCLE', ...
'OFFCENTRE_CIRCLE', ...
'CENTRE_SOURCE', ...
'CENTRE_SOURCE_2', ...
'SOURCE_SINK', ...
'SOURCE_SINK_2', ...
'SOURCE_SINK_2_GROWTH', ...
'SOURCE_SINK_2_GROWTH_BOWL' };
m.userdata.ranges.modelname.index = 9; % CLUSTER
end
modelname = m.userdata.ranges.modelname.range{m.userdata.ranges.modelname.index}; % CLUSTER
% More code for all iterations.
% Set priorities for simultaneous plotting of multiple morphogens, if desired.
% m = leaf_mgen_plotpriority( m, {'MGEN1', 'MGEN2'}, [1,2], [0.5,0.75] );
% Set colour of polariser gradient arrows.
% m = leaf_plotoptions(m,'highgradcolor',[0,0,0],'lowgradcolor',[1,0,0]);
%%% END OF USER CODE: INITIALISATION
%%% SECTION 1: ACCESSING MORPHOGENS AND TIME.
%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.
if isempty(m), return; end
setGlobals();
global gNEW_KA_PAR gNEW_KA_PER gNEW_KB_PAR gNEW_KB_PER
global gNEW_K_NOR gNEW_POLARISER gNEW_STRAINRET gNEW_ARREST
dt = m.globalProps.timestep;
polariser_i = gNEW_POLARISER;
P = m.morphogens(:,polariser_i);
[kapar_i,kapar_p,kapar_a,kapar_l] = getMgenLevels( m, 'KAPAR' );
[kaper_i,kaper_p,kaper_a,kaper_l] = getMgenLevels( m, 'KAPER' );
[kbpar_i,kbpar_p,kbpar_a,kbpar_l] = getMgenLevels( m, 'KBPAR' );
[kbper_i,kbper_p,kbper_a,kbper_l] = getMgenLevels( m, 'KBPER' );
[knor_i,knor_p,knor_a,knor_l] = getMgenLevels( m, 'KNOR' );
[strainret_i,strainret_p,strainret_a,strainret_l] = getMgenLevels( m, 'STRAINRET' );
[arrest_i,arrest_p,arrest_a,arrest_l] = getMgenLevels( m, 'ARREST' );
[id_centre_i,id_centre_p,id_centre_a,id_centre_l] = getMgenLevels( m, 'ID_CENTRE' );
[s_centre_i,s_centre_p,s_centre_a,s_centre_l] = getMgenLevels( m, 'S_CENTRE' );
[id_rim_i,id_rim_p,id_rim_a,id_rim_l] = getMgenLevels( m, 'ID_RIM' );
% Mesh type: circle
% circumpts: 24
% coneangle: 0
% dealign: 0
% height: 0
% innerpts: 0
% randomness: -0.1
% rings: 4
% version: 1
% xwidth: 2
% ywidth: 2
% Morphogen Diffusion Decay Dilution Mutant
% -------------------------------------------------
% KAPAR ---- ---- ---- ----
% KAPER ---- ---- ---- ----
% KBPAR ---- ---- ---- ----
% KBPER ---- ---- ---- ----
% KNOR ---- ---- ---- ----
% POLARISER ---- ---- ---- ----
% STRAINRET ---- ---- ---- ----
% ARREST ---- ---- ---- ----
% ID_CENTRE ---- ---- ---- ----
% S_CENTRE 0.5 ---- ---- ----
% ID_RIM ---- ---- ---- ----
%%% USER CODE: MORPHOGEN INTERACTIONS
% In this section you may modify the mesh in any way that does not
% alter the set of nodes.
if Steps(m)==0 % Initialisation code.
% Put any code here that should only be performed at the start of
% the simulation, for example, to set up initial morphogen values.
% m.nodes is the set of vertex positions, an N by 3 array if there
% are N vertices. Row number K contains the X, Y, and Z
% coordinates of the Kth vertex. To obtain a list of the X
% coordinates of every vertex, write m.nodes(:,1). The Y
% coordinates are given by m.nodes(:,2) and the Z coordinates by
% m.nodes(:,3).
switch modelname
case 'SQ_IN_CIRCLE'
SQUARE_RADIUS =0.5
is_centre_region = (abs(m.nodes(:,1))< SQUARE_RADIUS)...
& (abs(m.nodes(:,2))< SQUARE_RADIUS);
id_centre_p(is_centre_region) = 1
id_centre_l = id_centre_p * id_centre_a;
case 'CENTRE_OF_CIRCLE'
CENTRE_RADIUS = 0.5;
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
case 'OFFCENTRE_CIRCLE'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
case 'CENTRE_SOURCE'
CENTRE_RADIUS = 0.5;
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
% s_centre is produced by id_centre at a rate of 0.1.
% d(s_centre_p)/dt = 0.1*id_centre_l.
m.mgen_production( :, s_centre_i ) = 0.1*id_centre_l;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
case 'CENTRE_SOURCE_2'
CENTRE_RADIUS = 0.5;
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
m.morphogenclamp( id_centre_l > 0, s_centre_i) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
case 'SOURCE_SINK'
CENTRE_RADIUS = 0.5;
radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
case 'SOURCE_SINK_2'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
case 'SOURCE_SINK_2_GROWTH'
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
case 'SOURCE_SINK_2_GROWTH_BOWL'
m = leaf_setzeroz( m );
m = leaf_bowlz( m, -0.1 );
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
end
end
if false
figure(1);
plot3( m.nodes(m.tricellvxs,1)', ...
m.nodes(m.tricellvxs,2)', ...
s_centre_p(m.tricellvxs)' );
end
% Code for specific models.
switch modelname
case { 'SOURCE_SINK_2_GROWTH', 'SOURCE_SINK_2_GROWTH_BOWL' }
kapar_p = 0.1 * pro( 1, id_centre_l );
kbpar_p = kapar_p;
kaper_p = kapar_p;
kbper_p = kaper_p;
otherwise
% If this happens, maybe you forgot a model.
end
%%% END OF USER CODE: MORPHOGEN INTERACTIONS
%%% SECTION 3: INSTALLING MODIFIED VALUES BACK INTO MESH STRUCTURE
%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.
m.morphogens(:,polariser_i) = P;
m.morphogens(:,kapar_i) = kapar_p;
m.morphogens(:,kaper_i) = kaper_p;
m.morphogens(:,kbpar_i) = kbpar_p;
m.morphogens(:,kbper_i) = kbper_p;
m.morphogens(:,knor_i) = knor_p;
m.morphogens(:,strainret_i) = strainret_p;
m.morphogens(:,arrest_i) = arrest_p;
m.morphogens(:,id_centre_i) = id_centre_p;
m.morphogens(:,s_centre_i) = s_centre_p;
m.morphogens(:,id_rim_i) = id_rim_p;
%%% USER CODE: FINALISATION
% In this section you may modify the mesh in any way whatsoever.
%%% END OF USER CODE: FINALISATION
end
%%% USER CODE: SUBFUNCTIONS
% Here you may write any functions of your own, that you want to call from
% the interaction function, but never need to call from outside it.
% Remember that they do not have access to any variables except those
% that you pass as parameters, and cannot change anything except by
% returning new values as results.
% Whichever section they are called from, they must respect the same
% restrictions on what modifications they are allowed to make to the mesh.
% For example:
% function m = do_something( m )
% % Change m in some way.
% end
% Call it from the main body of the interaction function like this:
% m = do_something( m );
Ideal organistion of the code
To write this code more concisely the parts which are repeated between model variants can only be included once rather than being copied for each variant. The switch statements should only be used to include code that is not included in all of the models. The example code shown below produces the same output as the code used above but it has been made more concise.
As a further improvement to the code included above, in the code shown below, code which is needed for the initialisation, and that which is directing something that continues throughout the model has been separated. In the section headed by "if Steps(m)==0 % Setup code ", code specifying the initial state of the model should be written. Code which specifies an interaction that may change thruoghout the model, and code specifying growth parameters, should not be included in this initialisation section. Rather, any code which specifies something that continues throughout the model should be written after the " end " statement that ends the initialisation section. In the section after the initialisation, all code should be written under the sub-headings GRN, KRN or PRN (see the section about these headings below).
function m = gpt_circle_101118( m )
%m = gpt_circle_101118( m )
% Morphogen interaction function.
% Written at 2010-11-26 15:56:38.
% GFtbox revision 3285, 2010-11-26 14:21:47.664044.
% The user may edit any part of this function between delimiters
% of the form "USER CODE..." and "END OF USER CODE...". The
% delimiters themselves must not be moved, edited, deleted, or added.
if isempty(m), return; end
fprintf( 1, '%s found in %s\n', mfilename(), which(mfilename()) );
if exist( 'local_setproperties' )
m = local_setproperties( m );
end
realtime = m.globalDynamicProps.currenttime;
%%% USER CODE: INITIALISATION
% In this section you may modify the mesh in any way whatsoever.
if Steps(m)==0 % First iteration
% Zero out a lot of stuff to create a blank slate. If you want to use the
% GUI to set any of these things in the initial mesh, then you will need to
% comment out the corresponding lines here.
m.morphogens(:) = 0;
m.morphogenclamp(:) = 0;
m.mgen_production(:) = 0;
m.mgen_absorption(:) = 0;
m.seams(:) = false;
m.mgen_dilution(:) = false;
% Set up names for variant models. Useful for running multiple models on a cluster.
m.userdata.ranges.modelname.range = ...
{ 'CENTRE_OF_CIRCLE', ...
'CENTRE_SOURCE', ...
'CENTRE_SOURCE_2', ...
'SOURCE_SINK', ...
'SOURCE_SINK_2', ...
'SOURCE_SINK_2_GROWTH', ...
'SOURCE_SINK_2_GROWTH_BOWL' };
m.userdata.ranges.modelname.index = 7; % CLUSTER
end
modelname = m.userdata.ranges.modelname.range{m.userdata.ranges.modelname.index}; % CLUSTER
% More code for all iterations.
% Set priorities for simultaneous plotting of multiple morphogens, if desired.
% m = leaf_mgen_plotpriority( m, {'MGEN1', 'MGEN2'}, [1,2], [0.5,0.75] );
% Set colour of polariser gradient arrows.
% m = leaf_plotoptions(m,'highgradcolor',[0,0,0],'lowgradcolor',[1,0,0]);
%%% END OF USER CODE: INITIALISATION
%%% SECTION 1: ACCESSING MORPHOGENS AND TIME.
%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.
if isempty(m), return; end
setGlobals();
global gNEW_KA_PAR gNEW_KA_PER gNEW_KB_PAR gNEW_KB_PER
global gNEW_K_NOR gNEW_POLARISER gNEW_STRAINRET gNEW_ARREST
dt = m.globalProps.timestep;
polariser_i = gNEW_POLARISER;
P = m.morphogens(:,polariser_i);
[kapar_i,kapar_p,kapar_a,kapar_l] = getMgenLevels( m, 'KAPAR' );
[kaper_i,kaper_p,kaper_a,kaper_l] = getMgenLevels( m, 'KAPER' );
[kbpar_i,kbpar_p,kbpar_a,kbpar_l] = getMgenLevels( m, 'KBPAR' );
[kbper_i,kbper_p,kbper_a,kbper_l] = getMgenLevels( m, 'KBPER' );
[knor_i,knor_p,knor_a,knor_l] = getMgenLevels( m, 'KNOR' );
[strainret_i,strainret_p,strainret_a,strainret_l] = getMgenLevels( m, 'STRAINRET' );
[arrest_i,arrest_p,arrest_a,arrest_l] = getMgenLevels( m, 'ARREST' );
[id_centre_i,id_centre_p,id_centre_a,id_centre_l] = getMgenLevels( m, 'ID_CENTRE' );
[s_centre_i,s_centre_p,s_centre_a,s_centre_l] = getMgenLevels( m, 'S_CENTRE' );
[id_rim_i,id_rim_p,id_rim_a,id_rim_l] = getMgenLevels( m, 'ID_RIM' );
% Mesh type: circle
% circumpts: 24
% coneangle: 0
% dealign: 0
% height: 0
% innerpts: 0
% randomness: -0.1
% rings: 4
% version: 1
% xwidth: 2
% ywidth: 2
% Morphogen Diffusion Decay Dilution Mutant
% -------------------------------------------------
% KAPAR ---- ---- ---- ----
% KAPER ---- ---- ---- ----
% KBPAR ---- ---- ---- ----
% KBPER ---- ---- ---- ----
% KNOR ---- ---- ---- ----
% POLARISER ---- ---- ---- ----
% STRAINRET ---- ---- ---- ----
% ARREST ---- ---- ---- ----
% ID_CENTRE ---- ---- ---- ----
% S_CENTRE 0.5 ---- ---- ----
% ID_RIM ---- ---- ---- ----
%%% USER CODE: MORPHOGEN INTERACTIONS
% In this section you may modify the mesh in any way that does not
% alter the set of nodes.
if Steps(m)==0 % Setup code.
% Put any code here that should only be performed at the start of
% the simulation, for example, to set up initial morphogen values.
% m.nodes is the set of vertex positions, an N by 3 array if there
% are N vertices. Row number K contains the X, Y, and Z
% coordinates of the Kth vertex. To obtain a list of the X
% coordinates of every vertex, write m.nodes(:,1). The Y
% coordinates are given by m.nodes(:,2) and the Z coordinates by
% m.nodes(:,3).
switch modelname
case { 'CENTRE_OF_CIRCLE', 'CENTRE_SOURCE', ...
'CENTRE_SOURCE_2', 'SOURCE_SINK' }
CENTRE_RADIUS = 0.5;
CENTRE_POSITION = [ 0, 0 ];
case { 'SOURCE_SINK_2', 'SOURCE_SINK_2_GROWTH' }
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
case 'SOURCE_SINK_2_GROWTH_BOWL'
m = leaf_setzeroz( m );
m = leaf_bowlz( m, -0.1 );
CENTRE_RADIUS = 0.2;
CENTRE_POSITION = [ 0.4, 0 ];
end
radii = sqrt( (m.nodes(:,1) - CENTRE_POSITION(1)).^2 + ...
(m.nodes(:,2) - CENTRE_POSITION(2)).^2 );
id_centre_p(radii <= CENTRE_RADIUS) = 1;
id_centre_l = id_centre_p * id_centre_a;
rimnodes = radii > max(radii)*0.8;
id_rim_p( rimnodes ) = 1;
id_rim_l = id_rim_p * id_rim_a;
end
switch modelname
case 'CENTRE_SOURCE'
% @@GRN Gene Regulatory Network
% s_centre is produced by id_centre at a rate of 0.1.
% d(s_centre_p)/dt = 0.1*id_centre_l.
m.mgen_production( :, s_centre_i ) = 0.1*id_centre_l;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
case 'CENTRE_SOURCE_2'
% @@GRN Gene Regulatory Network
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
m.morphogenclamp( id_centre_l > 0, s_centre_i) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 10 );
case { 'SOURCE_SINK', 'SOURCE_SINK_2' }
% @@GRN Gene Regulatory Network
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
case 'SOURCE_SINK_2_GROWTH'
% @@GRN Gene Regulatory Network
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
% @@KRN Growth Regulatory Network
kapar_p = 0.1 * pro( 1, id_centre_l );
kbpar_p = kapar_p;
kaper_p = kapar_p;
kbper_p = kaper_p;
case 'SOURCE_SINK_2_GROWTH_BOWL'
% @@GRN Gene Regulatory Network
% s_centre is initially 1 everywhere that id_centre is
% present, and is held fixed at that value.
s_centre_p( id_centre_l > 0 ) = 1;
s_centre_l = s_centre_p * s_centre_a;
m.morphogenclamp( id_centre_l > 0, s_centre_i ) = 1;
% s_centre is initially 0 everywhere that id_rim is
% present, and is held fixed at that value.
m.morphogenclamp( id_rim_l > 0, s_centre_i ) = 1;
% s_centre decays everywhere at a constant rate
% proportional to its concentration.
m = leaf_mgen_absorption( m, s_centre_i, 0 );
% @@KRN Growth Regulatory Network
kapar_p = 0.1 * pro( 1, id_centre_l );
kbpar_p = kapar_p;
kaper_p = kapar_p;
kbper_p = kaper_p;
end
if false
figure(1);
plot3( m.nodes(m.tricellvxs,1)', ...
m.nodes(m.tricellvxs,2)', ...
s_centre_p(m.tricellvxs)' );
end
%%% END OF USER CODE: MORPHOGEN INTERACTIONS
%%% SECTION 3: INSTALLING MODIFIED VALUES BACK INTO MESH STRUCTURE
%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.
m.morphogens(:,polariser_i) = P;
m.morphogens(:,kapar_i) = kapar_p;
m.morphogens(:,kaper_i) = kaper_p;
m.morphogens(:,kbpar_i) = kbpar_p;
m.morphogens(:,kbper_i) = kbper_p;
m.morphogens(:,knor_i) = knor_p;
m.morphogens(:,strainret_i) = strainret_p;
m.morphogens(:,arrest_i) = arrest_p;
m.morphogens(:,id_centre_i) = id_centre_p;
m.morphogens(:,s_centre_i) = s_centre_p;
m.morphogens(:,id_rim_i) = id_rim_p;
%%% USER CODE: FINALISATION
% In this section you may modify the mesh in any way whatsoever.
%%% END OF USER CODE: FINALISATION
end
%%% USER CODE: SUBFUNCTIONS
% Here you may write any functions of your own, that you want to call from
% the interaction function, but never need to call from outside it.
% Remember that they do not have access to any variables except those
% that you pass as parameters, and cannot change anything except by
% returning new values as results.
% Whichever section they are called from, they must respect the same
% restrictions on what modifications they are allowed to make to the mesh.
% For example:
% function m = do_something( m )
% % Change m in some way.
% end
% Call it from the main body of the interaction function like this:
% m = do_something( m );
Lesson 2: Specifying anisotropic growth using the interaction function
PRN, GRN, KRN
To maximise the ease with which the code written in the interaction function can be related to the biological function it represents, code should be written under one of three headings which describes how it is influencing growth.
All code specifying interactions between factors in the model which do not directly influence the polariser or growth rates should be written under the heading GRN, which stands for "gene regulatory network". For example, if an identity region produces a diffusible signal in a given model, the code specifying this should be written in a GRN section.
Code which specifies growth rates, for example by assigning values to kapar, kaper etc., should be written under the heading KRN.
Code which specifies the setting up of the polariser, for example by directing production / decay of the polariser, should be written under the heading PRN, which stands for "polariser regulatory network".
Polariser gradients
In order for anisotropic growth to be specified, a polariser gradient must be created across the canvas to provide directional information.
One way to create a gradient of polariser is to have production of polariser in a restricted region coupled with decay of the polariser everywhere. When this method is used, it is possible for the polariser gradient to become very shallow and somewhat randomised in some regions which creates problems for specifying growth. Biologically, there must be a limit to the size of the polariser gradient that a cell can detect. To overcome these problems with shallow polariser gradients, in regions where shallow gradients are present, GFTbox can be used to either set the polariser gradient to zero, or to fix the direction of the polariser.
There are two different ways that the steepness of an exponential gradient can be measured. The relative gradient describes the percentage change in the concentration of a chemical over a fixed distance. Between any two points a fixed distance apart along an exponential gradient of a chemical, the percentage change in concentration will be the same, so the relative gradient will be the same everywhere. The absolute gradient describes the actual difference in concentration between one point and another (this could, for example be the difference in the number of molecules between one side of a cell and another).
Below code is presented which specifies the production of polariser in a central circular identity region, with decay of polariser throughout the canvas. The concentration of the polariser is clamped to a fixed level in the central identity region. When the absolute value of the polariser gradient drops below a threshold, the polariser is fixed to have the same direction that it has where the gradient is steeper. There is an initial growth-free set-up period which allows the polariser gradient to become established before growth starts.
Code which is not part of the interaction function template (code that is specific to this model) is highlighted in bold.
% Section 1 function m = gpt_polarised_101126( m ) %m = gpt_polarised_101126( m ) % Morphogen interaction function. % Written at 2010-11-29 12:26:00. % GFtbox revision 3285, 2010-11-26 14:21:47.664044. % The user may edit any part of this function between delimiters % of the form "USER CODE..." and "END OF USER CODE...". The % delimiters themselves must not be moved, edited, deleted, or added. if isempty(m), return; end fprintf( 1, '%s found in %s\n', mfilename(), which(mfilename()) ); if exist( 'local_setproperties' ) m = local_setproperties( m ); end realtime = m.globalDynamicProps.currenttime; % Section 2 %%% USER CODE: INITIALISATION % In this section you may modify the mesh in any way whatsoever. if Steps(m)==0 % First iteration % Zero out a lot of stuff to create a blank slate. If you want to use the % GUI to set any of these things in the initial mesh, then you will need to % comment out the corresponding lines here. m.morphogens(:) = 0; m.morphogenclamp(:) = 0; m.mgen_production(:) = 0; m.mgen_absorption(:) = 0; m.seams(:) = false; m.mgen_dilution(:) = false; % Set up names for variant models. Useful for running multiple models on a cluster. m.userdata.ranges.modelname.range = { ... 'CENTRE_POL' }; m.userdata.ranges.modelname.index = 1; % CLUSTER end modelname = m.userdata.ranges.modelname.range{m.userdata.ranges.modelname.index}; % CLUSTER switch modelname case 'CENTRE_POL' % Set up the parameters (e.g. mutations) for this model here. otherwise % If you reach here, you probably forgot a case. end % More code for all iterations. % Set priorities for simultaneous plotting of multiple morphogens, if desired. % m = leaf_mgen_plotpriority( m, {'MGEN1', 'MGEN2'}, [1,2], [0.5,0.75] ); % Set colour of polariser gradient arrows. % m = leaf_plotoptions(m,'highgradcolor',[0,0,0],'lowgradcolor',[1,0,0]); %%% END OF USER CODE: INITIALISATION % Section 3 %%% SECTION 1: ACCESSING MORPHOGENS AND TIME. %%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT. if isempty(m), return; end setGlobals(); global gNEW_KA_PAR gNEW_KA_PER gNEW_KB_PAR gNEW_KB_PER global gNEW_K_NOR gNEW_POLARISER gNEW_STRAINRET gNEW_ARREST dt = m.globalProps.timestep; polariser_i = gNEW_POLARISER; P = m.morphogens(:,polariser_i); [kapar_i,kapar_p,kapar_a,kapar_l] = getMgenLevels( m, 'KAPAR' ); [kaper_i,kaper_p,kaper_a,kaper_l] = getMgenLevels( m, 'KAPER' ); [kbpar_i,kbpar_p,kbpar_a,kbpar_l] = getMgenLevels( m, 'KBPAR' ); [kbper_i,kbper_p,kbper_a,kbper_l] = getMgenLevels( m, 'KBPER' ); [knor_i,knor_p,knor_a,knor_l] = getMgenLevels( m, 'KNOR' ); [strainret_i,strainret_p,strainret_a,strainret_l] = getMgenLevels( m, 'STRAINRET' ); [arrest_i,arrest_p,arrest_a,arrest_l] = getMgenLevels( m, 'ARREST' ); [id_centre_i,id_centre_p,id_centre_a,id_centre_l] = getMgenLevels( m, 'ID_CENTRE' ); % Mesh type: circle % circumpts: 96 % coneangle: 0 % dealign: 0 % height: 0 % innerpts: 0 % randomness: 0.1 % rings: 16 % version: 1 % xwidth: 2 % ywidth: 2 % Morphogen Diffusion Decay Dilution Mutant % ------------------------------------------------- % KAPAR ---- ---- ---- ---- % KAPER ---- ---- ---- ---- % KBPAR ---- ---- ---- ---- % KBPER ---- ---- ---- ---- % KNOR ---- ---- ---- ---- % POLARISER 0.01 0.1 ---- ---- % STRAINRET ---- ---- ---- ---- % ARREST ---- ---- ---- ---- % ID_CENTRE ---- ---- ---- ---- %%% USER CODE: MORPHOGEN INTERACTIONS % In this section you may modify the mesh in any way that does not % Section 4 % alter the set of nodes. if Steps(m)==0 % Setup code. switch modelname case { 'CENTRE_POL' } % Make a polariser. CENTRE_RADIUS = 0.3; % here a circular central identity region % is being specified as was done in the % examples above. radii = sqrt( m.nodes(:,1).^2 + m.nodes(:,2).^2 ); id_centre_p(radii <= CENTRE_RADIUS) = 1; % @@PRN Polariser Regulatory Network %specifies the diffusion rate of polariser m = leaf_mgen_conductivity( m, 'POLARISER', 0.01 ); % specifies degradation rate of polariser m = leaf_mgen_absorption( m, 'POLARISER', 0.1 ); % below, the function leaf_setproperty is used to fix the % polariser gradient when it drops below an absolute % value of 0.002 % the minimum gradient beyond which fixing is done m = leaf_setproperty( m, ... 'mingradient', 0.002, ... ... % setting relativepolgrad to false specifies the ... % absolute gradient should be measured 'relativepolgrad', false, ... ... % setting relativepolgrad to false specifies the ... % absolute gradient should be measured 'usefrozengradient', true ... ... % setting usefrozengradient to true specifies ... % that the polariser should be fixed in the direction ... % it has where the gradient is steeper. ); otherwise % If you reach here, you probably forgot a case. end end GROWTH_START_TIME = 4.9; % the delay time at the beginning of the simulation switch modelname case { 'CENTRE_POL', } % @@model CENTRE_POL % @@PRN Polariser Regulatory Network % this clamps the polariser concentration where % id_centre is present m.morphogenclamp( id_centre_p==1, polariser_i ) = 1; P = 0.5 * id_centre_p;% polariser value is 0.5* the value of id_centre-p otherwise % If you reach here, you probably forgot a case. end if realtime > GROWTH_START_TIME % if the simulation time (realtime) passes the GROWTH_START_TIME % growth rates will apply switch modelname case 'CENTRE_POL' % @@model CENTRE_POL kapar_p(:) = 0.05; % growth parallel to the polariser % is greater than growth perpendicular kaper_p(:) = 0; kbpar_p = kapar_p; kbper_p = kaper_p; knor_p(:) = 0; otherwise % If you reach here, you probably forgot a case. end end % Section 5 %%% END OF USER CODE: MORPHOGEN INTERACTIONS %%% SECTION 3: INSTALLING MODIFIED VALUES BACK INTO MESH STRUCTURE %%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT. m.morphogens(:,polariser_i) = P; m.morphogens(:,kapar_i) = kapar_p; m.morphogens(:,kaper_i) = kaper_p; m.morphogens(:,kbpar_i) = kbpar_p; m.morphogens(:,kbper_i) = kbper_p; m.morphogens(:,knor_i) = knor_p; m.morphogens(:,strainret_i) = strainret_p; m.morphogens(:,arrest_i) = arrest_p; m.morphogens(:,id_centre_i) = id_centre_p; %%% USER CODE: FINALISATION % In this section you may modify the mesh in any way whatsoever. %%% END OF USER CODE: FINALISATION end %%% USER CODE: SUBFUNCTIONS % Section 6 function m = local_setproperties( m ) % This function is called at time zero in the INITIALISATION section of the % interaction function. It provides commands to set each of the properties % that are contained in m.globalProps. Uncomment whichever ones you would % like to set yourself, and put in whatever value you want. % % Some of these properties are for internal use only and should never be % set by the user. At some point these will be moved into a different % component of m, but for the present, just don't change anything unless % you know what it is you're changing. %lots of code appears here but doesn't need to be modified so it has been left out here end % Section 7 % Here you may write any functions of your own, that you want to call from % the interaction function, but never need to call from outside it. % Remember that they do not have access to any variables except those % that you pass as parameters, and cannot change anything except by % returning new values as results. % Whichever section they are called from, they must respect the same % restrictions on what modifications they are allowed to make to the mesh.
Simulation
To run the simulation, use the region at the bottom of the GUI called Run. You can either press the Step button to progress the simulation one step at a time, or you can run the simulation for a defined number of steps, for a defined time, or until the canvas reaches a particular increase in area.
The step size for the simulation can be controlled in the simulation section of the GUI, in the box that says Timescale. As a rule of thumb, growth rate * time step should be less than 0.01.