AAMToolbox viewing statistical model: Difference between revisions
Jump to navigation
Jump to search
Created page with 'Back to Tutorial pages<br> =<span style="color:Navy;">Viewing shape and appearance models in 2D</span>= ==Principle component analy…' |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Tutorials on the Shape modelling toolbox#1|Back to Tutorial pages]]<br> | [[Tutorials on the Shape modelling toolbox#1|Back to Tutorial pages]]<br> | ||
=<span style="color:Navy;">Viewing shape and appearance models in 2D</span>= | =<span style="color:Navy;">Viewing shape and appearance models in 2D</span>= | ||
== | |||
=<span style="color:Navy;">Walking through contributions of principle components.</span>= | |||
=<span style="color: | <br><br> | ||
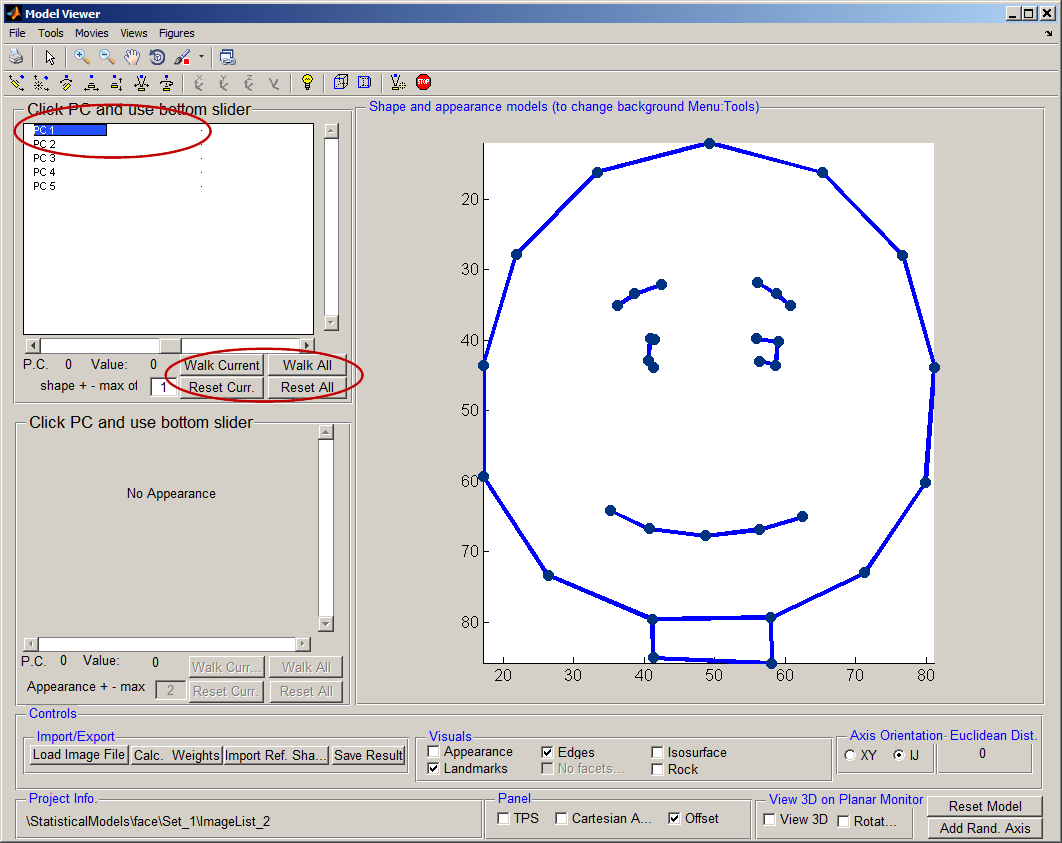
[[File:Walk_model_AAMToolbox.png|700px|Model Viewer]]<br><br> | |||
===<span style="color:FireBrick;">Mean shape</span>=== | |||
{| border="0" cellpadding="5" cellspacing="3" | |||
|- valign="top" | |||
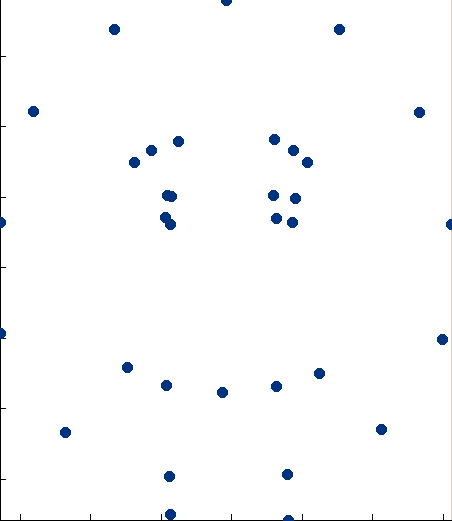
|width="700pt"|The dots on the right represent the mean positions of the landmarks averaged over all the images in the model. These points mean more to us once they are joined by lines (see above screenshot). Capturing that higher meaning requires more analysis or, as in this case, human interaction (when we created the template).<br><br>Note that the point models had been normalised to the''' same scale, same rotation and same translational''' position.<br> | |||
|width="200pt"|[[File:Mean_shape.png|200px|The Model generator control panel]] | |||
=<span style="color: | |} | ||
===<span style="color:FireBrick;">Variations along the principle component axis</span>=== | |||
{| border="0" cellpadding="5" cellspacing="3" | |||
[[File: | |- valign="top" | ||
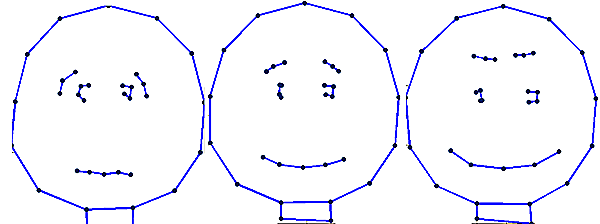
== | |width="700pt"|To visualise sliding (walking) along an axis imagine a straight line fitted to a set of data points. Then read-out the x,y coordinates as we move back and forth along the line. Correlation between x and y (the straight line) means that the outputs are correlated. In this model we are doing a similar thing as we slide along the axis (fitted line) we read-out values in the model coordinate system that are then transformed (by the model) back into the viewing coordinates. <br><br>[[File:PC1_cartoon_combined.png|200px|The Model generator control panel]]<br> Left, minus one standard deviation along PC1.<br>Middle, mean shape. <br>Right, plus one standard deviation along PC1. | ||
===<span style="color:FireBrick;"> | |width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">CartoonPC1.flv|CartoonPC1.png</wikiflv><br>Sliding (walking) along the principle component axis. | ||
[[File: | |} | ||
===<span style="color:FireBrick;">Variations along axis with the next largest variation</span>=== | |||
{| border="0" cellpadding="5" cellspacing="3" | |||
|- valign="top" | |||
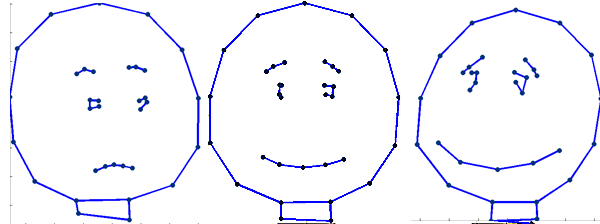
|width="700pt"|<br><br>[[File:PC1_cartoon_combined2.png|200px|+1 and -1 standard deviation from the mean]]<br> Left, minus one standard deviation along PC2.<br>Middle, mean shape. <br>Right, plus one standard deviation along PC2. | |||
|width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">CartoonPC2.flv|CartoonPC2.png</wikiflv><br>Sliding (walking) along the axis accounting for the second most amount of variation. | |||
|} | |||