AAMToolbox viewing statistical model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 17: | Line 17: | ||
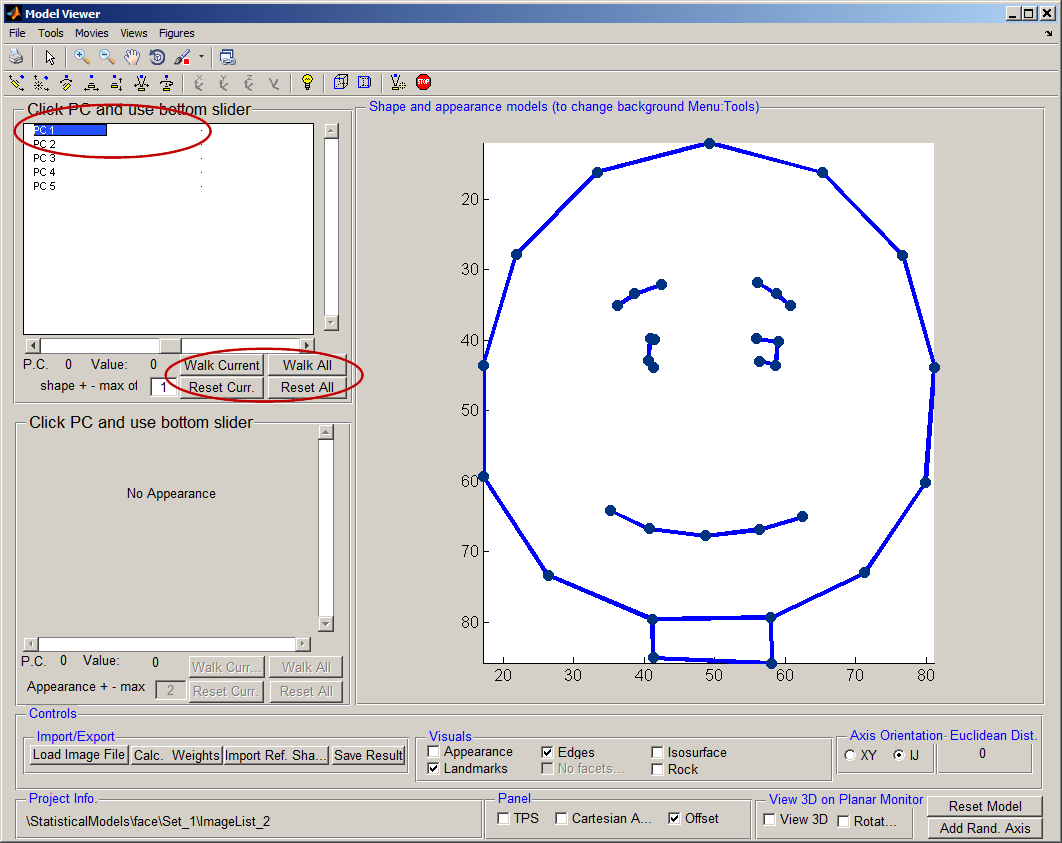
|width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">Movie-2012-02-15t10-48-49.flv|Movie-2012-02-15t10-23-17 First.png</wikiflv><br>Sliding (walking) along the principle component axis. | |width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">Movie-2012-02-15t10-48-49.flv|Movie-2012-02-15t10-23-17 First.png</wikiflv><br>Sliding (walking) along the principle component axis. | ||
|} | |} | ||
Movie-2012-02-15t10-23- | ===<span style="color:FireBrick;">Variations along other axes</span>=== | ||
{| border="0" cellpadding="5" cellspacing="3" | |||
|- valign="top" | |||
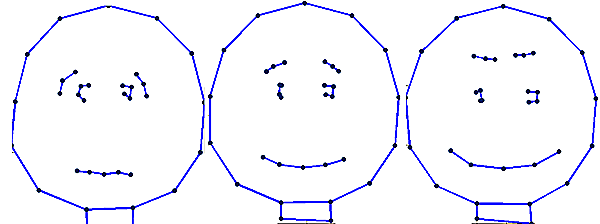
|width="700pt"|<br><br>[[File:PC1_cartoon_combined.png|200px|The Model generator control panel]]<br> Left, minus one standard deviation along PC1.<br>Middle, mean shape. <br>Right, plus one standard deviation along PC1. | |||
|width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">Movie-2012-02-15t10-48-49.flv|Movie-2012-02-15t10-23-17 First.png</wikiflv><br>Sliding (walking) along the principle component axis. | |||
|} | |||
===<span style="color:FireBrick;">Sliding through shape space</span>=== | |||
{| border="0" cellpadding="5" cellspacing="3" | |||
|- valign="top" | |||
|width="700pt"|<br><br>[[File:PC1_cartoon_combined.png|200px|The Model generator control panel]]<br> Left, minus one standard deviation along PC1.<br>Middle, mean shape. <br>Right, plus one standard deviation along PC1. | |||
|width="300pt"|<wikiflv width="300" height="300" logo="false" loop="true" background="white">Movie-2012-02-15t10-48-49.flv|Movie-2012-02-15t10-23-17 First.png</wikiflv><br>Sliding (walking) along the principle component axis. | |||
|} | |||