AAMToolbox viewing statistical model
Viewing shape and appearance models in 2D
Principle component analysis of point-models and image pixel values (appearance models)
To view results from the PCA select 'View Stats Model from the AAMToolbox control panel:
View shape models
- Shape model
- Input: landmark points, i.e. the point-models for all images of interest.
- Output: mean shape and associated shape model that captures deviations from the mean. Enough principle components are included to account for 95% of the variance from the mean (set using Options).
- Appearance model
- Input: landmark points, i.e. the point-models together with the image intensity within triangles determined by a Delauny triangulation of the points.
- Output: mean appearance and associated appearance model that captures deviations from the mean.
Statistical Model Generator control panel.
Showing the steps (in red) to build a statistical model.
Notice: the set of landmarks represented as stars will be included in the shape model, in this case all of them. For this model you can accept the default settings and jump directly to step 3 and select all the images. Then compute the principle component analysis (PCA) using step 4 and return to the AAMToolbox on the way to viewing the results.
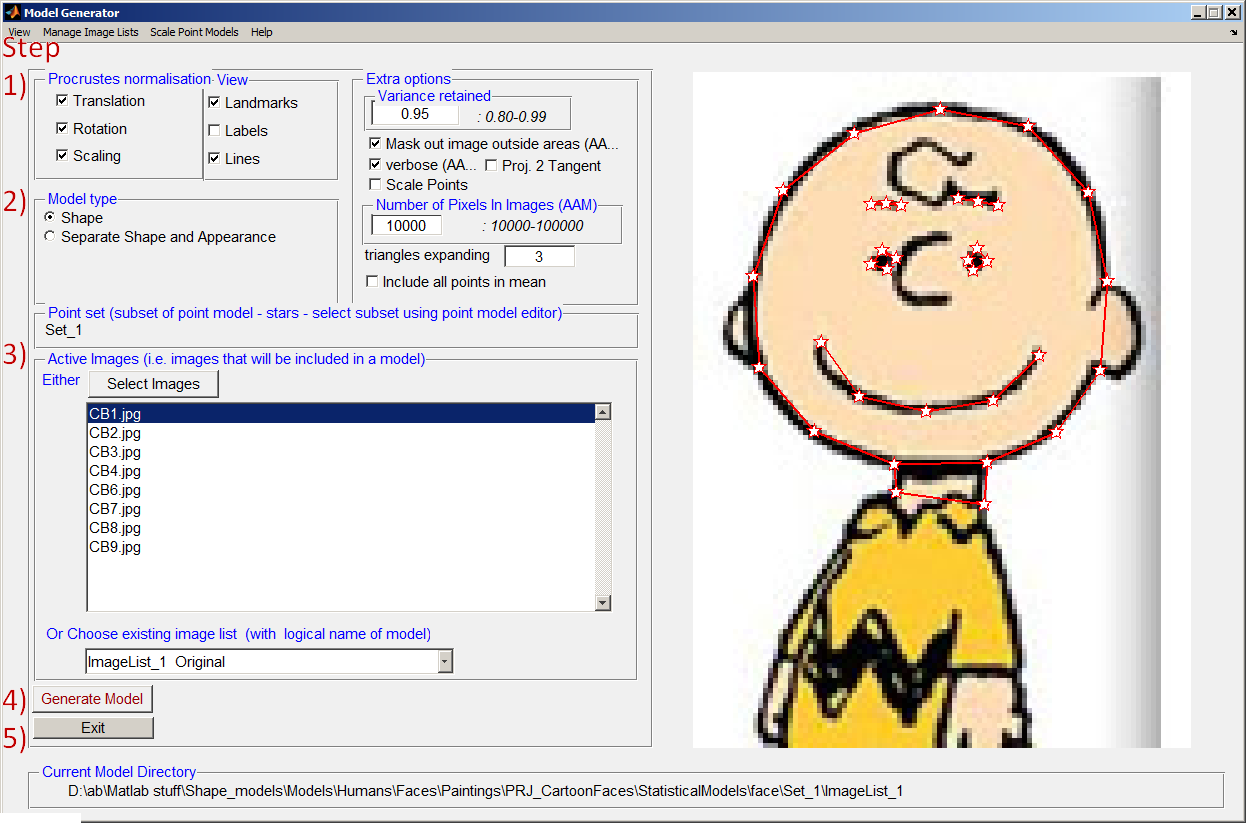
Steps to build a shape model using principle component analysis (PCA)
Step 1) Options
- The first step in PCA is to align all the point models. In this case we assume that the images should be normalised to the same scale, same rotation and same translational position. This might not always be the case. If we want to model leaf growth then the point model should not be scaled. Alternatively, if we want to capture the pose of a face portrait the point models should not be rotationally aligned.
For the cartoon faces we normalise for all three.
