Details on hydrophobicity plots

Back to MSERs etc

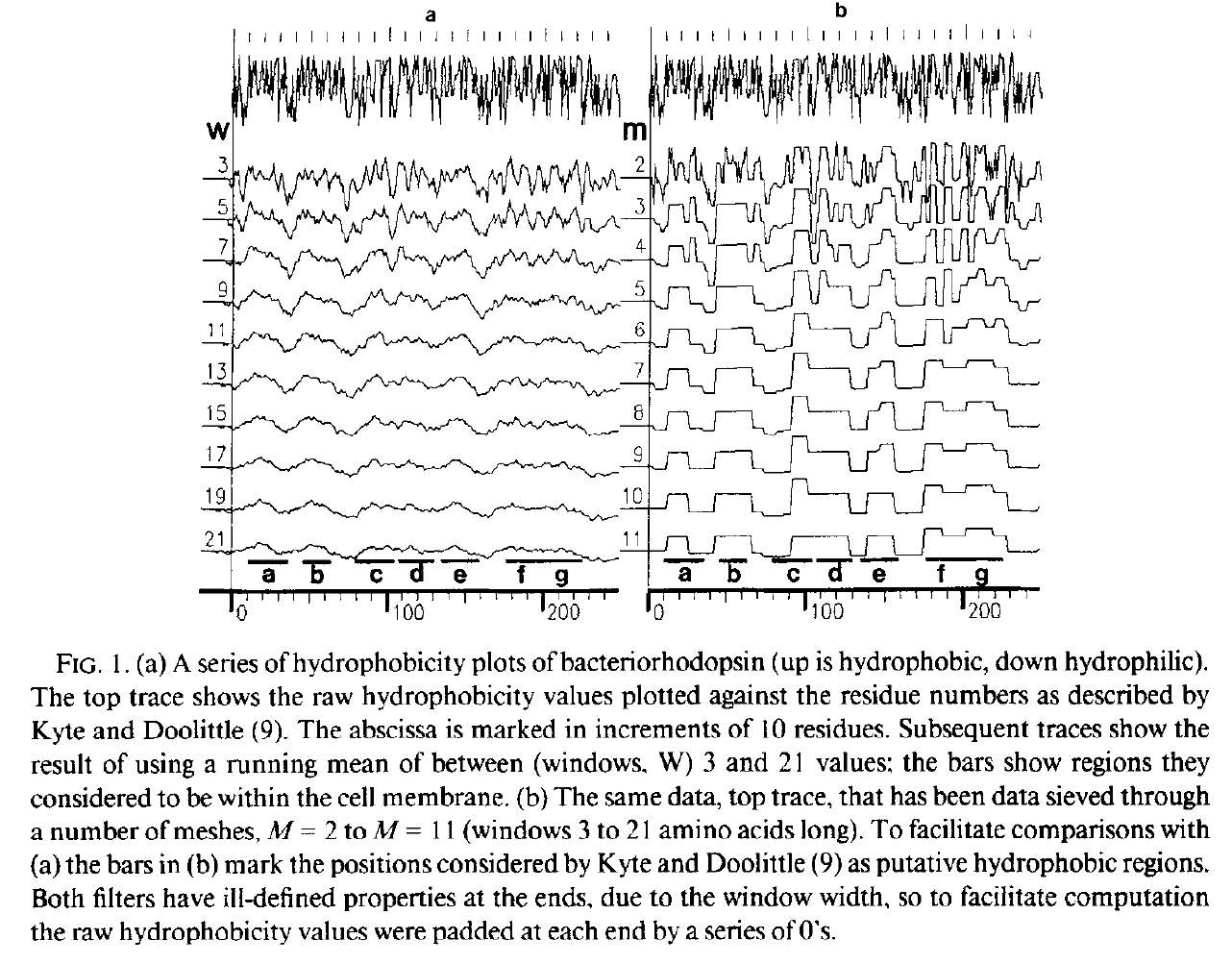
Trying to spot regions (lengths) that are up (hydrophobic) and down (hydrophilic)

Left: Running mean (c.f Gaussian): no good, Right: Median based Data-sieve: much better Bangham, J.A. (1988) Data-sieving hydrophobicity plots. Anal. Biochem. 174, 142–145

Abstract

Hydrophobicity plots provide clues to the tertiary structure of proteins (J. Kyte and R. F. Doolittle, 1982, J. Mol. Biol.157, 105; C. Chothia, 1984, Annu. Rev. Biochem.53, 537; T. P. Hopp and K. R. Woods, 1982, Proc. Natl. Acad. Sci. USA78, 3824). To render domains more visible, the raw data are usually smoothed using a running mean of between 5 and 19 amino acids. This type of smoothing still incorporates two disadvantages. First, peculiar residues that do not share the properties of most of the amino acids in the domain may prevent its identification. Second, as a low-pass frequency filter the running mean smoothes sudden transitions from one domain, or phase, to another. Data-sieving is described here as an alternative method for identifying domains within amino acid sequences. The data-sieve is based on a running median and is characterized by a single parameter, the mesh size, which controls its resolution. It is a technique that could be applied to other series data and, in multidimensions, to images in the same way as a median filter.

Actually, for the data-sieve I did use a cascade of medians which was a very inefficient algorithm. Subsequently, I switched to a cascade of 1D recursive medians which also preserved scale space but was hugely quicker and is idempotent.

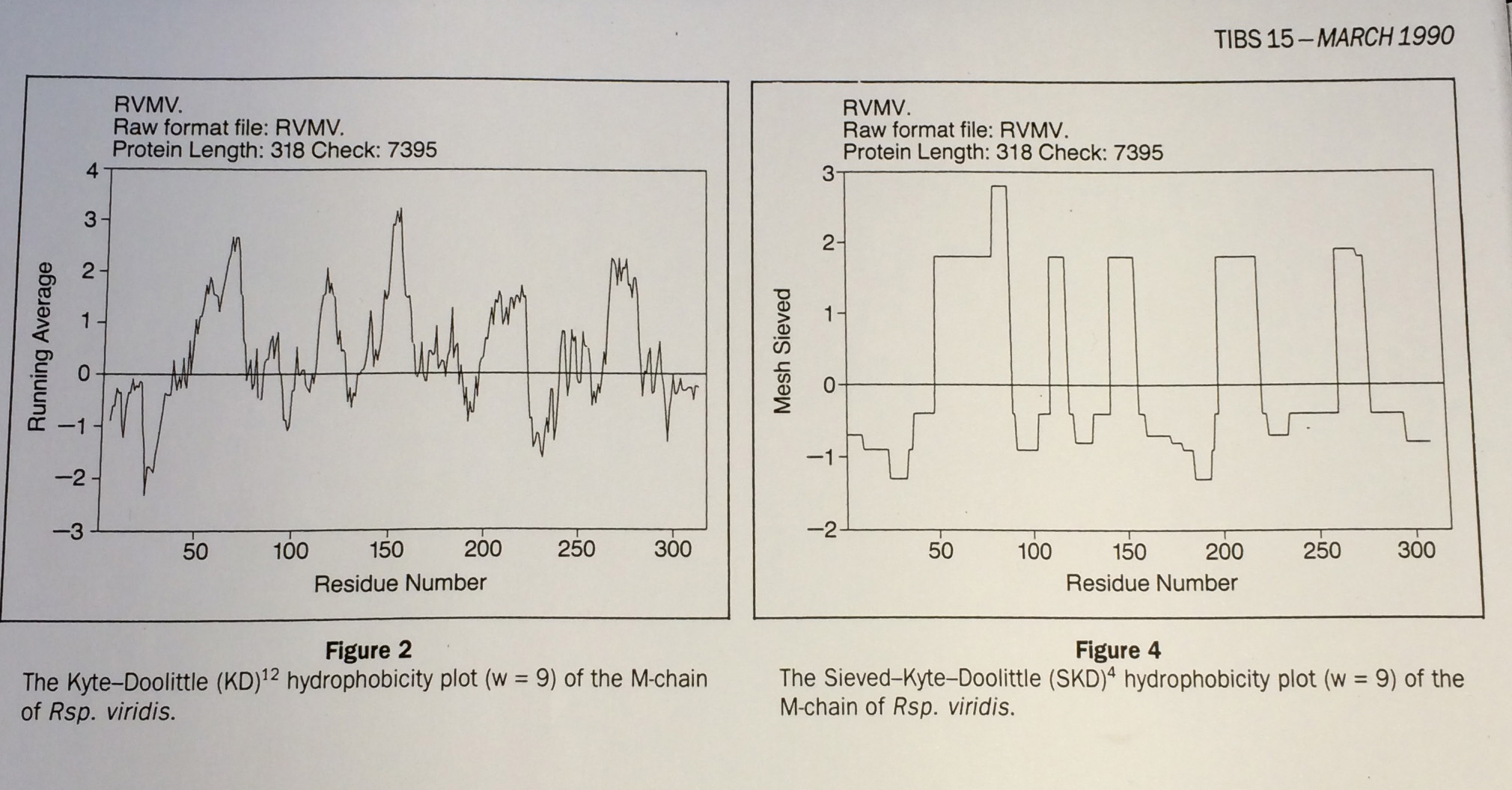
From Fasman and Gilbert "The prediction of transmembrane protein sequences and their conformation: an evaluation" in Trends in Biochemistry 15 pp 89:91 Left: Running mean (c.f Gaussian): no good, Right: Median based Data-sieve: much better

These authors compared many different methods and concluded that the data-sieve was best. However, they found a reason not to recommend it: that they didn't understand how it worked.

Well there you are then. Means verses medians.

Actually, there are some simple computational issues here. At the time computers were only just becoming commonplace and they were not (by current standards) powerful. Computing a running mean is very easy. Choose a window size, n, and start by adding up all the values in the first n samples to make S. Divide by n and you have the first point. Now move along by one value - add the new value to S, subtract the first (the outgoing) value from S and divide by n again. Add, subtract, divide: easy and the size of n does not matter. The median is harder, it requires a sort of some type. But I discovered a neat alternative, the recursive median ('m') sieve, indeed I found a family of such filter banks with different kernels 'o', 'c', 'M', 'N', and 'm' and called them all sieves.

They are also trivial to compute in 1D.

Don't give up, get motivated

The good thing was that I was motivated to prove exactly how it worked and why it was so good - I moved to Computing Sciences and published everything in computing journals. Where computer scientists would find it - or not - think MSER literature.

I was also so excited about the discovery of a new set of transforms that could underpin brain vision that I attended conferences on vision - the amazing Horace Barlow's retirement bash, the 6 month extravaganza: Computer Vision at the Isaac Newton Institute for Mathematical Sciences (University of Cambridge, United Kingdom) July to December, 1993. Organised by scientists that I greatly admire: David Mumford (Harvard), Andrew Blake, Brian Ripley (Oxford)etc. However, it was difficult. A typical remark was 'But mathematicians have shown that Gaussian Filter banks are unique ...' The focus was anisotropic diffusion.

I was proving that they were not unique. They are unique among linear filters but not filters in general.

The non-linear filters I was describing held the promise of extremely useful properties in computer vision - as it turns out one example could be the MSER.