Time: tradeoff: Difference between revisions

From BanghamLab
Jump to navigation Jump to search
(Created page with "Return to GFtbox hints and tips<br><br> ==Choosing a timestep that is short enough to be accurate and yet not take too long to compute...")
 
No edit summary
Line 4: Line 4:
{| border=" " cellpadding="5" cellspacing="5"
{| border=" " cellpadding="5" cellspacing="5"
|- valign="top"
|- valign="top"
|width="200px"|[[File:GPT_DemoSubdivision_20121116-000000-0002.png|200px|GFtbox interface]]Simple mesh of 382 elements equally spaced vertices. Superimposed are the polarity arrows (pointing bottom left) and purple and blue factors that control local growth rates.
|width="200px"|[[File:GPT_DemoSubdivision_DT_1B.jpg|200px|GFtbox interface]]Step size (dt) is 10. '''Is the 'S' shape correct?'''<br><br> Simple mesh of 382 elements equally spaced vertices. Superimposed are the polarity arrows (pointing bottom left) and purple and blue factors that control local growth rates.
|width="200px"|[[File:GPT_DemoSubdivision_20121116-000010-0001.png|200px|GFtbox interface]]After one step in which the central region is subdivided twice (the vertices are too dense to see).
|width="200px"|[[File:GPT DemoSubdivision DT 2B.jpg|200px|GFtbox interface]]Step size (dt) is 1. '''Is the 'S' shape correct?''' It is different so we reduce it again...
|width="200px"|[[File:GPT_DemoSubdivision_20121116-000010-0002.png|200px|GFtbox interface]]As for the previous example but the size of the triangles forming the mesh is only visible along the edge. Red marks regions of increased growth on the top and bottom surfaces.
|width="200px"|[[File:GPT_DemoSubdivision_DT_3B.jpg|200px|GFtbox interface]]Step size (dt) is 0.1. This shape is very similar to the previous one so we might conclude that it is not necessary to make the stepsize this short, a stepsize of 1 is OK.
|}
|}
{| border=" " cellpadding="5" cellspacing="5"
It still might not be correct because the mesh itself could be too coarse.
|- valign="top"
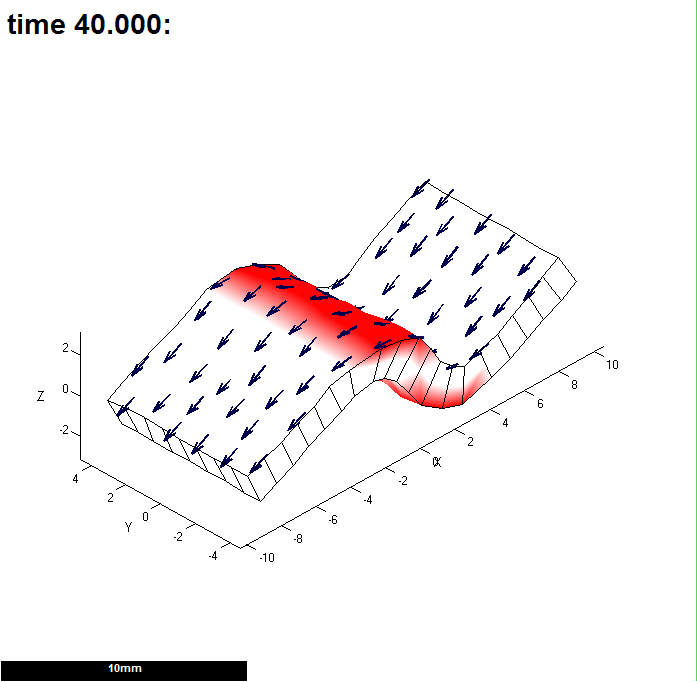
|width="200px"|[[File:GPT_DemoSubdivision_20121116-000040-0001.png|200px|GFtbox interface]]After growing for 40 steps the excess growth has bent the canvas into an 'S' shape. '''Note the smooth bend''' is associated with about 4 elements.
|width="200px"|[[File:GPT_DemoSubdivision_20121116-000040-0002.png|200px|GFtbox interface]]As for the previous example, but there has been no subdivision and the curves are unacceptably incomplete and jagged. There should '''always be enough elements to permit curves to develop smoothly'''.
|}
===Tutorial===
Run the project ([http://cmpdartsvr1.cmp.uea.ac.uk/downloads/software/GPT_DemoSubdivision_20121116.zip <span style="color: Navy">example project </span>])for 40 steps to see the effect of:
#subdivision
Then change the modelname to 'NOSUBDIVISION', i.e. make a change to the interaction function
        % Set up names for variant models.  Useful for running multiple models on a cluster.
        m.userdata.ranges.modelname.range = { 'NOSUBDIVISION', 'WITHSUBDIVISION' };  % CLUSTER
        m.userdata.ranges.modelname.index = 2;                      % CLUSTER
by setting index to 1. With too few elements, bends are jagged.
<br><br>
<br><br>
The interaction function is shown below, red highlights the region of interest.
<span style="color: CornflowerBlue"></span>
function m = gpt_demosubdivision_20121116( m )
<span style="color: Green">%m = gpt_demosubdivision_20121116( m )</span>
<span style="color: Green">%  Morphogen interaction function.</span>
<span style="color: Green">%  Written at 2012-11-16 12:30:06.</span>
<span style="color: Green">%  GFtbox revision 4351, .</span>
<span style="color: Green">% The user may edit any part of this function between delimiters</span>
<span style="color: Green">% of the form "USER CODE..." and "END OF USER CODE...".  The</span>
<span style="color: Green">% delimiters themselves must not be moved, edited, deleted, or added.</span>
    if isempty(m), return; end
    fprintf( 1, '<span style="color: Green">%s found in %s\n', mfilename(), which(mfilename()) );</span>
    try
        m = local_setproperties( m );
    catch
    end
    realtime = m.globalDynamicProps.currenttime;
<span style="color: CornflowerBlue"></span>
<span style="color: Green">%%% USER CODE: INITIALISATION</span>
<span style="color: Green">% In this section you may modify the mesh in any way whatsoever.</span>
    if (Steps(m)==0) && m.globalDynamicProps.doinit <span style="color: Green">% First iteration</span>
        <span style="color: Green">% Zero out a lot of stuff to create a blank slate.  </span>
        <span style="color: Green">% If no morphogens are set in the GUI it may be useful to</span>
        <span style="color: Green">% zero some arrays by uncommenting the following.</span>
        <span style="color: Green">% m.morphogens(:) = 0;</span>
        <span style="color: Green">% m.morphogenclamp(:) = 0;</span>
        <span style="color: Green">% m.mgen_production(:) = 0;</span>
        <span style="color: Green">% m.mgen_absorption(:) = 0;</span>
        <span style="color: Green">% m.seams(:) = false;</span>
        <span style="color: Green">% m.mgen_dilution(:) = false;</span>
        <span style="color: Green">% Set up names for variant models.  Useful for running multiple models on a cluster.</span>
        m.userdata.ranges.modelname.range = { 'NOSUBDIVISION', 'WITHSUBDIVISION' };  <span style="color: Green">% CLUSTER</span>
        m.userdata.ranges.modelname.index = 1;                      <span style="color: Green">% CLUSTER</span>
    end
    modelname = m.userdata.ranges.modelname.range{m.userdata.ranges.modelname.index};  <span style="color: Green">% CLUSTER</span>
   
    disp(sprintf('\nRunning <span style="color: Green">%s model %s\n',mfilename, modelname));    </span>
    <span style="color: Green">% to plot polariser on the A side and resultant areal growth rate on the B side:</span>
    m = leaf_plotoptions( m, 'morphogenA', 'KAPAR', 'morphogenB', 'KBPAR' );
<span style="color: Green">%%% END OF USER CODE: INITIALISATION</span>
<span style="color: CornflowerBlue"></span>
<span style="color: Green">%%% SECTION 1: ACCESSING MORPHOGENS AND TIME.</span>
<span style="color: Green">%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.</span>
    if isempty(m), return; end
    setGlobals();
    global gNEW_KA_PAR gNEW_KA_PER gNEW_KB_PAR gNEW_KB_PER
    global gNEW_K_NOR gNEW_POLARISER gNEW_STRAINRET gNEW_ARREST
    dt = m.globalProps.timestep;
    polariser_i = gNEW_POLARISER;
    P = m.morphogens(:,polariser_i);
    [kapar_i,kapar_p,kapar_a,kapar_l] = getMgenLevels( m, 'KAPAR' );
    [kaper_i,kaper_p,kaper_a,kaper_l] = getMgenLevels( m, 'KAPER' );
    [kbpar_i,kbpar_p,kbpar_a,kbpar_l] = getMgenLevels( m, 'KBPAR' );
    [kbper_i,kbper_p,kbper_a,kbper_l] = getMgenLevels( m, 'KBPER' );
    [knor_i,knor_p,knor_a,knor_l] = getMgenLevels( m, 'KNOR' );
    [strainret_i,strainret_p,strainret_a,strainret_l] = getMgenLevels( m, 'STRAINRET' );
    [arrest_i,arrest_p,arrest_a,arrest_l] = getMgenLevels( m, 'ARREST' );
    [id_a_i,id_a_p,id_a_a,id_a_l] = getMgenLevels( m, 'ID_A' );
    [id_b_i,id_b_p,id_b_a,id_b_l] = getMgenLevels( m, 'ID_B' );
    [id_subdivide_i,id_subdivide_p,id_subdivide_a,id_subdivide_l] = getMgenLevels( m, 'ID_SUBDIVIDE' );
<span style="color: Green">% Mesh type: rectangle</span>
<span style="color: Green">%            base: 0</span>
<span style="color: Green">%          centre: 0</span>
<span style="color: Green">%      randomness: 0.1</span>
<span style="color: Green">%        version: 1</span>
<span style="color: Green">%          xdivs: 16</span>
<span style="color: Green">%          xwidth: 16</span>
<span style="color: Green">%          ydivs: 8</span>
<span style="color: Green">%          ywidth: 8</span>
<span style="color: Green">%            Morphogen    Diffusion  Decay  Dilution  Mutant</span>
<span style="color: Green">%            --------------------------------------------------</span>
<span style="color: Green">%                KAPAR        ----    ----      ----    ----</span>
<span style="color: Green">%                KAPER        ----    ----      ----    ----</span>
<span style="color: Green">%                KBPAR        ----    ----      ----    ----</span>
<span style="color: Green">%                KBPER        ----    ----      ----    ----</span>
<span style="color: Green">%                KNOR        ----    ----      ----    ----</span>
<span style="color: Green">%            POLARISER        ----    ----      ----    ----</span>
<span style="color: Green">%            STRAINRET        ----    ----      ----    ----</span>
<span style="color: Green">%              ARREST        ----    ----      ----    ----</span>
<span style="color: Green">%                ID_A        ----    ----      ----    ----</span>
<span style="color: Green">%                ID_B        ----    ----      ----    ----</span>
<span style="color: Green">%        ID_SUBDIVIDE        ----    ----      ----    ----</span>
<span style="color: Green">%%% USER CODE: MORPHOGEN INTERACTIONS</span>
<span style="color: Green">% In this section you may modify the mesh in any way that does not</span>
<span style="color: CornflowerBlue"></span>
<span style="color: Green">% alter the set of nodes.</span>
    if (Steps(m)==0) && m.globalDynamicProps.doinit  <span style="color: Green">% Initialisation code.</span>
        <span style="color: Green">% Put any code here that should only be performed at the start of</span>
        <span style="color: Green">% the simulation, for example, to set up initial morphogen values.</span>
        id_a_p((m.nodes(:,1)>0)&(m.nodes(:,1)<=2))=1;
        id_b_p((m.nodes(:,1)>-2)&(m.nodes(:,1)<=0))=1;
        id_subdivide_p((m.nodes(:,1)>=-2)&(m.nodes(:,1)<=2))=1;
        P=m.nodes(:,1);
    end
    if realtime<=1
        kapar_p(:) = 0;
        kaper_p(:) = 0;
        kbpar_p(:) = 0;
        kbper_p(:) = 0;
        knor_p(:)  = 0;
    else
        kapar_p(:) = 0.05*id_a_p;
        kaper_p(:) = 0;
        kbpar_p(:) = 0.05*id_b_p;
        kbper_p(:) = 0;
        knor_p(:)  = 0;
    end
<span style="color: CornflowerBlue"></span>
<span style="color: Green">%%% END OF USER CODE: MORPHOGEN INTERACTIONS</span>
<span style="color: Green">%%% SECTION 3: INSTALLING MODIFIED VALUES BACK INTO MESH STRUCTURE</span>
<span style="color: Green">%%% AUTOMATICALLY GENERATED CODE: DO NOT EDIT.</span>
    m.morphogens(:,polariser_i) = P;
    m.morphogens(:,kapar_i) = kapar_p;
    m.morphogens(:,kaper_i) = kaper_p;
    m.morphogens(:,kbpar_i) = kbpar_p;
    m.morphogens(:,kbper_i) = kbper_p;
    m.morphogens(:,knor_i) = knor_p;
    m.morphogens(:,strainret_i) = strainret_p;
    m.morphogens(:,arrest_i) = arrest_p;
    m.morphogens(:,id_a_i) = id_a_p;
    m.morphogens(:,id_b_i) = id_b_p;
    m.morphogens(:,id_subdivide_i) = id_subdivide_p;
<span style="color: Green">%%% USER CODE: FINALISATION</span>
<span style="color: Green">% In this section you may modify the mesh in any way whatsoever.</span>
    switch modelname
        case 'NOSUBDIVISION'
            <span style="color: Red">% do nothing</span>
        case 'WITHSUBDIVISION'
            <span style="color: Red">% subdivide on the first step</span>
            if realtime>0 && realtime<=0+dt
                m = leaf_subdivide( m, 'morphogen','id_subdivide',...
                    'min',0.5,'max',1,...
                    'mode','mid','levels','all');
            end
            if realtime>0 && realtime<=0+dt
                m = leaf_subdivide( m, 'morphogen','id_subdivide',...
                    'min',0.5,'max',1,...
                    'mode','mid','levels','all');
            end
        otherwise
            <span style="color: Green">% If this happens, maybe you forgot a model.</span>
    end
<span style="color: Green">%%% END OF USER CODE: FINALISATION</span>
end
<span style="color: Green">%%% USER CODE: SUBFUNCTIONS</span>
<span style="color: CornflowerBlue"></span>
function m = local_setproperties( m )
<span style="color: Green">% This function is called at time zero in the INITIALISATION section of the</span>
<span style="color: Green">% interaction function.  It provides commands to set each of the properties</span>
<span style="color: Green">% that are contained in m.globalProps.  Uncomment whichever ones you would</span>
<span style="color: Green">% like to set yourself, and put in whatever value you want.</span>
<span style="color: Green">%</span>
<span style="color: Green">% Some of these properties are for internal use only and should never be</span>
<span style="color: Green">% set by the user.  At some point these will be moved into a different</span>
<span style="color: Green">% component of m, but for the present, just don't change anything unless</span>
<span style="color: Green">% you know what it is you're changing.</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'trinodesvalid', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'prismnodesvalid', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'thicknessRelative', 1.600000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'thicknessArea', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'thicknessMode', 'physical' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'activeGrowth', 1.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'displayedGrowth', 1.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'displayedMulti', [] );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowNegativeGrowth', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'usePrevDispAsEstimate', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'perturbInitGrowthEstimate', 0.000010 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'perturbRelGrowthEstimate', 0.010000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'perturbDiffusionEstimate', 0.000100 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'resetRand', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'mingradient', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'relativepolgrad', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'usefrozengradient', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'userpolarisation', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'thresholdsq', 4.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'splitmargin', 1.400000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'splitmorphogen', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'thresholdmgen', 0.500000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bulkmodulus', 1.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'unitbulkmodulus', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'poissonsRatio', 0.300000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'starttime', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'timestep', 0.010000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'timeunitname', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'distunitname', 'mm' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'scalebarvalue', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'validateMesh', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'rectifyverticals', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowSplitLongFEM', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'longSplitThresholdPower', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowSplitBentFEM', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowSplitBio', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowFlipEdges', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowElideEdges', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'mincellangle', 0.200000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'alwaysFlat', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'flattenforceconvex', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'flatten', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'flattenratio', 1.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'useGrowthTensors', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'plasticGrowth', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'totalinternalrotation', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'stepinternalrotation', 2.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'showinternalrotation', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'performinternalrotation', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'internallyrotated', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'maxFEcells', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'inittotalcells', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bioApresplitproc', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bioApostsplitproc', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'maxBioAcells', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'colors', (6 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'colorvariation', 0.050000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'colorparams', (12 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'biocolormode', 'auto' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'freezing', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'canceldrift', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'mgen_interaction', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'mgen_interactionName', 'gpt_demosubdivision_20121116' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowInteraction', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'interactionValid', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'gaussInfo', (unknown type ''struct'') );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'stitchDFs', [] );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'D', (36 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'C', (36 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'G', (6 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'solver', 'cgs' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'solverprecision', 'double' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'solvertolerance', 0.001000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'solvertolerancemethod', 'max' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'diffusiontolerance', 0.000010 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowsparse', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'maxIters', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'maxsolvetime', 1000.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'cgiters', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'simsteps', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'stepsperrender', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'growthEnabled', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'diffusionEnabled', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'flashmovie', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'makemovie', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'moviefile', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'codec', 'None' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'autonamemovie', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'overwritemovie', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'framesize', [] );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'mov', [] );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'boingNeeded', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'initialArea', 128.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bendunitlength', 11.313708 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'targetRelArea', 1.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'defaultinterp', 'min' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'readonly', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'projectdir', 'D:\ab\Matlab stuff\Growth models' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'modelname', 'GPT_DemoSubdivision_20121116' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'allowsave', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'addedToPath', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bendsplit', 0.300000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'usepolfreezebc', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'dorsaltop', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'defaultazimuth', -45.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'defaultelevation', 33.750000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'defaultroll', 0.000000 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'defaultViewParams', (unknown type ''struct'') );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'comment', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'legendTemplate', '%T: %q\n%m' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bioAsplitcells', true );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bioApullin', 0.142857 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'bioAfakepull', 0.202073 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'interactive', false );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'coderevision', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'coderevisiondate', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'modelrevision', 0 );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'modelrevisiondate', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'savedrunname', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'savedrundesc', '' );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'vxgrad', (108 values) );</span>
<span style="color: Green">%    m = leaf_setproperty( m, 'lengthscale', 16.000000 );</span>
end
<span style="color: CornflowerBlue"></span>
<span style="color: Green">% Here you may write any functions of your own, that you want to call from</span>
<span style="color: Green">% the interaction function, but never need to call from outside it.</span>
<span style="color: Green">% Remember that they do not have access to any variables except those</span>
<span style="color: Green">% that you pass as parameters, and cannot change anything except by</span>
<span style="color: Green">% returning new values as results.</span>
<span style="color: Green">% Whichever section they are called from, they must respect the same</span>
<span style="color: Green">% restrictions on what modifications they are allowed to make to the mesh.</span>
<span style="color: Green">% For example:</span>
<span style="color: CornflowerBlue"></span>
<span style="color: Green">% function m = do_something( m )</span>
<span style="color: Green">%  % Change m in some way.</span>
<span style="color: Green">% end</span>
<span style="color: Green">% Call it from the main body of the interaction function like this:</span>
<span style="color: Green">%      m = do_something( m );</span>

Revision as of 11:08, 6 December 2012

Return to GFtbox hints and tips

Choosing a timestep that is short enough to be accurate and yet not take too long to compute

There is a tradeoff between speed and the accuracy with which the equation solver can solve the equations. This is feature of all numerical modelling. Continuous time is approximated by a series of short intervals or steps (dt). With steps that are too long the mesh will grow more than about 2% - an acceptable limit. Very short steps take a long time to compute and can also suffer rounding problems. This is an example of subdividing a rectangular mesh in the region in which curves will develop.

GFtbox interfaceStep size (dt) is 10. Is the 'S' shape correct?

Simple mesh of 382 elements equally spaced vertices. Superimposed are the polarity arrows (pointing bottom left) and purple and blue factors that control local growth rates. 		GFtbox interfaceStep size (dt) is 1. Is the 'S' shape correct? It is different so we reduce it again... GFtbox interfaceStep size (dt) is 0.1. This shape is very similar to the previous one so we might conclude that it is not necessary to make the stepsize this short, a stepsize of 1 is OK.

It still might not be correct because the mesh itself could be too coarse.

Retrieved from "http://cmpdartsvr3-v.uea.ac.uk/wiki/BanghamLab/index.php?title=Time:_tradeoff&oldid=6078"